What will you learn in this Article?
- What are the basic directions
- What are the various types of questions asked in this topic
- How to approach the various types of questions
ExamConnect
Directions is one of those topics which is repeatedly seen as the examiners favourite and the questions regarding the same is seen across examinations so one learning and the mastering this topic to minimize the time take to solve is crucial.
In a typical directions question, the examinee is given a starting position and is given a series of instructions regarding the movement from the starting point to an endpoint and he/she is expected to tell relative distance and direction from the starting point to the end point.
Basics of Directions
There are four main directions namely North, South, East and West. Also, there are four cardinal directions which are in between the main directions like north-east, north-west, south-east and south-west.
Types of Questions
Generally, we can be asked four types of questions under this topic:
- Shortest distance between 2 points
- Position of a point in respective of the other point
- Shadow type questions
- Rotation based questions
Note: The left or right of an individual depends of the direction they are facing.
Let’s look at all these types with the help of examples:
1. Shortest distance between two points
In these types of questions, the examinee is provided with numeric values of the distance travelled in different directions and he/she is expected to find the shortest distance between the starting and the endpoint.
For finding the shortest distance, it is necessary to know the Pythagoras Theorem, which says
(Base)2 + (Perpendicular)2 = (Hypotenuse)2
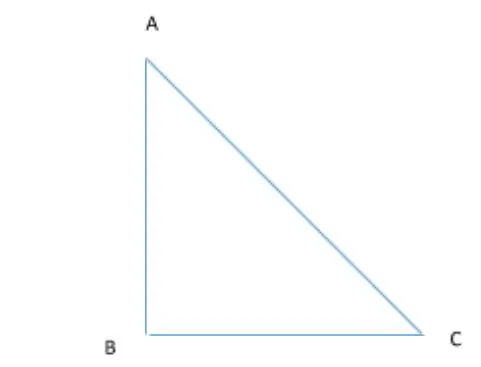
i.e. (AB)2 + (BC)2 = (AC)2
Hence for the shortest distance (AC) = √((AB)2 +(BC)2)
Example Question: A man walked 4km south, turned right and walk for 1 km, turned North and walked 10km, then he turned east and walked 9km. How far is he from the starting point?
- 6 km C) 10 km
- 8 km D) 12 km
Solution: Firstly, we will trace the man’s steps in a diagram to ease up calculations and eliminate any chance of a mistake.
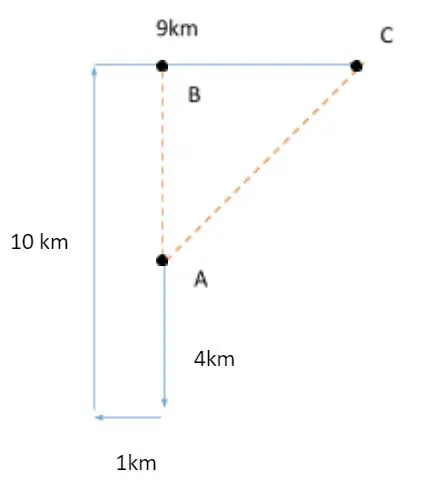
In the diagram, A is the initial point and C is the final point. Now we have to find AC. We will first find the values of AC and BC and then use Pythagoras theorem to find value of AC.
Value of AB and BC is 6km and 8km respectively, because the figure formed on the left side of the triangle is a rectangle with opposite sides being equal to one another.
Using Pythagoras theorem, 8^2 + 6^2 = AC^2. Thus AC = 10 km
Try out these questions yourself for a deeper understanding of the topic.
Q1 A person drives 20 km east. He then takes a left turn and drives 7 km after which he goes 12 km towards the west. Next, he takes a right turn and drives 5 km. Finally, he takes left and drives 8km. How far is he from the starting point?
- 10 km C) 16 km
- 12 km D) 13 km
Q2 Sita move towards South-east a distance of 7 m, then she moves towards the west and travels a distance of 14 m. From here, she moves towards North-west a distance of 7 m and finally, she moves a distance of 4 m towards the east and stood at that point. How far is she from the starting point?
- 4 m C) 3 m
- 11 m D) 10 m
Solutions:
Ans1. B)
Ans2. D)
2. Position of a point with respect to other point
In these types of questions, the examinee is given a starting point and a series of instructions directing him/her towards an endpoint and he/she has to find out the relative position of the ending point from the starting point or vice-a-versa.
It is advised to make a diagram for every “direction” question to ease up the calculation and save up the crucial time.
Example Question: A rat runs 20m towards east and turns right, runs 10m and turns right, runs 7m and again turns to left, runs 5m and turns to the left and finally runs 12m. In which direction is the rat, with respect to its initial position?
- South-East C) South
- South- West D) North-West
Solution: Firstly, we will trace the rat’s steps in a diagram in order to ease up calculations and eliminate any chance of a mistake.
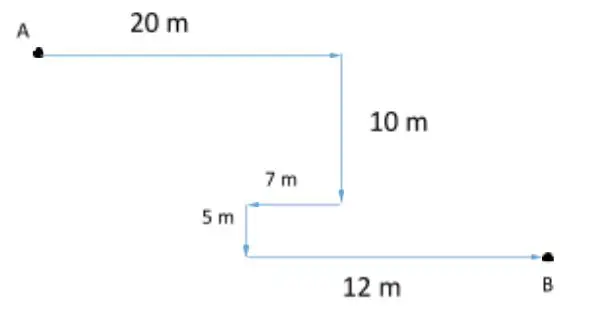
In this diagram, A is the initial point and B is the final point. We have to find the relative position of point B with respect to point A. As we can see, point B is located south-east of point A. So the answer is A.
Try this concept out yourself!
Q3. Ritu is facing north. She then goes to her right and moves to the south. While facing south, she then goes to her left-hand direction and then again moves to the south. She again takes a left turn and then a right turn. Finally, she goes towards the east and then moves to her right.
- In which direction is Ritu now, with respect to her initial position?
- In which direction is the starting point with respect to the ending point?
Solution:
Ans3. (a) South-East (b) North-West
3. Concept of Shadows
The sun rises from the east in the morning and sets in the west in the afternoon, as we know shadows are formed opposite to the light source we can say that
- In the morning, the shadow will fall on the west because of the eastward rise of the sun.
- In the evening, the shadow will fall on the east because of the westward fall of the sun.
Example Question: In the morning, while jogging, I noticed that my shadow was right behind me. So in which direction was I Jogging?
Solution: First of all, we know that I was jogging in the morning, which means that the shadow would fall on the west. Since the shadow was right behind me, that means that I was jogging in the East.
4.1 Rotation of Directions
In these types of questions, we are given a series of instructions about the changes in the position of directions caused by rotation and we have to determine new sets of direction.
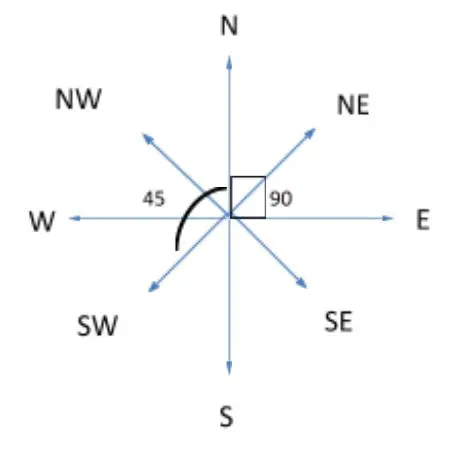
Note: If let’s say North rotates by 90 degrees anti-clockwise, then all the other direction will also rotate 90 degrees anti-clockwise.
Example Question: If ‘South’ becomes ‘North-East’ then what will ‘west’ become?
Solution: In the above question, north-east rotates by 135 degrees anti-clockwise and replaces the south. So other direction will also rotate by the same angle in the same manner. Therefore, we can clearly see that ‘west’ has become ‘north-east’.
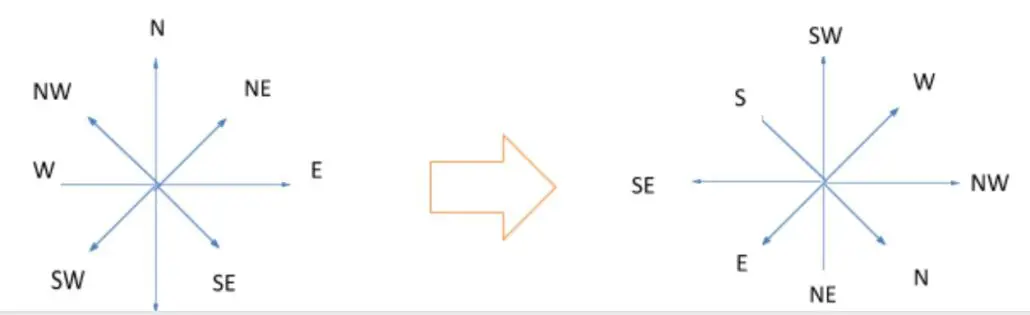
4.2 Rotation of individuals
In these types of questions, we will be given a series of instructions regarding the rotation of an individual and we have to find the direction they would be facing after the rotations.
Example Question: A man is facing east. He turns 45 degrees anticlockwise and then another 180 degrees anticlockwise and then 270 degrees in the clockwise direction. Which direction is he facing now?
Solution: The man first rotates 45 degrees in the anti-clockwise direction and then 180 anti-clockwise i.e. 225 degrees in the anticlockwise direction. After that, he went 270 degrees in the clockwise direction, which nets out to be 45 degrees clockwise. Therefore, we can say that the man rotated 45 degrees clockwise which means he must be facing south-east.
