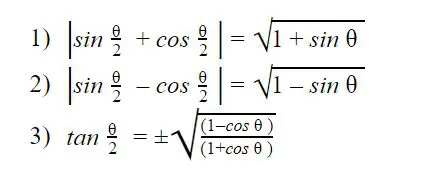Higher Maths | Trigonometry #3 | Basic Concepts and Important Formulae

What will you learn in this article?

This article is the final article in our series: Higher Maths | Trigonometry

• Addition and Subtraction of Trigonometric Functions
• Formulae for changing product into sum or differences and vice-versa
• Multiple angles and Submultiple angles along with formulae

Previous Article

Before reading this article, do go through trigonometry article 1 and article 2 for a better understanding of the Higher Maths | Trigonometry topic for entrance exams.

Addition and Subtraction of Trigonometric Functions

There are 7 general formulae that is used in addition and subtraction of trigonometric functions. These formulae are:

1. sin (A±B) = sin A cos B ± cos A sin B
2. cos (A±B) = cos A cos B ± sin A sin B
3. tan (A±B) = (tan A ± tan B) / (1∓tan A tan B)
4. cot (A±B) = (cot A cot B ∓ 1)/ (cot B ± cot A)
5. sin (A+B) sin (A-B) =A -B =B -A
6. cos (A+B) cos (A-B) =A -B =B -A
7. tan (A+B+C) = (tan A +tan B +tan C -tan A tan B tan C) / (1-tan A tan B -tan B tan C -tan C tan A)

Formulae for changing product into sum or difference and vice-versa

Now, some questions are asked in competitive exams, where you’ll have to find the sum or difference of trigonometric functions when it is given in product form. For this, there are 4 formulae that we can use. They are:

1. 2 sin A cos B = sin (A+B) +sin (A-B)
2. 2 cos A sin B = sin (A+B) -sin (A-B)
3. 2 cos A cos B = cos (A+B) +cos (A-B)
4. 2 sin A sin B = cos (A-B) -cos (A+B)

So, these are the formulae to change product into sum or difference. But, sometimes this might be asked in the reverse way. That is, you’ll have to find the product from a given sum or difference between trigonometric functions. To do that, we have another set of 4 formulae. They are:

1. sin A + sin B =2 sin (A+B)/2 cos (A-B)/2
2. sin A – sin B =2 cos (A+B)/2 sin (A-B)/2
3. cos A + cos B =2 cos (A+B)/2 cos (A-B)/2
4. cos A – cos B =2 sin (A+B)/2 sin (B-A)/2

Multiple and Sub-multiple angles

Multiple angles are basically the angles that we use generally, which are given as a single non fraction unit. For example, sin A is a trigonometric function with multiple angle. On the other hand, Sub-Multiple angles are those which are given in fractional format. For example, sin A/2 is a trigonometric function with sub-multiple angle.

Formulae for Multiple Angles

We can define 9 formulae for multiple angles. They are:

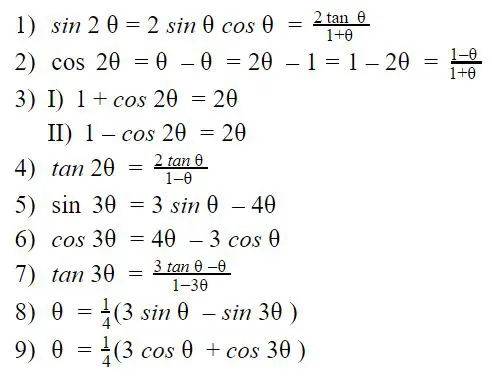
Formulae for sub-multiple angles

We can define 3 formulae for sub-multiple angles. They are: